第13课算法分析基础¶

13.1 到底什么才是算法？¶

狭义地说，我们此处说的算法是：是用计算机解决问题的方法、步骤。但是广义上来说，算法可以是解决一切问题的计算方法。

13.2 算法的特性¶

输入：一个算法必须有零个或以上输入量。
输出：一个算法应有一个或以上输出量，输出量是算法计算的结果。
明确性：算法的描述必须无歧义，以保证算法的实际执行结果是精确地符合要求或期望，通常要求实际运行结果是确定的。
有限性：依据图灵的定义，一个算法是能够被任何图灵完备系统模拟的一串运算，而图灵机只有有限个状态、有限个输入符号和有限个转移函数（指令）。而一些定义更规定算法必须在有限个步骤内完成任务。
有效性：又称可行性。能够实现，算法中描述的操作都是可以通过已经实现的基本运算执行有限次来实现。

来源：维基百科 - 算法词条

13.3 算法如何表示？¶

13.3.1 伪代码(Pseudocode)¶

简单的说就是用一种比较结构化的自然语言（通常是英语，当然也可以是中文）和符号来进行算法过程的描述。它介于自然语言与程序设计语言之间，主要用于描述算法，程序员可以对照伪代码很方便的转换为相应程序的代码。

请看下面的简单例子

输入3个数，打印输出其中最大的数。可用如下的伪代码表示：

则我们可以写出伪代码：

BEGIN
    INPUT A，B，C
    IF A > B THEN A -> Max
    ELSE B -> Max
    IF C > Max THEN C ->Max
    PRINT Max
END

当然，我们也可以用中文写出伪代码

程序开始
    输入 A, B, C
    如果 A 大于 B 则 A 赋值给 Max
    否则 B 赋值给 Max
    如果 C 大于 Max 则 C 赋值给 Max
    打印 Max
程序结束

根据伪代码，可以很快写出Python代码

a = int(input())
b = int(input())
c = int(input())

max = 0
if a > b:
    max = a
else:
    max = b

if c > max:
    max = c
print(max)

小伙伴们，可以尝试先写出思路和步骤，其实也很类似伪代码，然后可以很快就对照写出Python代码。在生活中，除非你需要出版书籍，或者撰写论文，我们很少写严谨的伪代码，但是下面要介绍的流程图对你非常有用。

13.3.2 流程图(FlowChart)¶

流程图是一种专门用图形化的方法去描述算法的方法。因为其形象直观，所以应用很广泛。

首先看看上节伪代码示例中流程图的例子：

流程图例子

当然，流程图不仅仅可以用于表示算法的思路，同样在日常工作与学习的流程中也可以使用。请看下面的例子：

流程图例子2

画流程图时，需要遵守一些基本的规则，下面我们就简单的介绍流程图的使用方法。

13.3.2.1 流程图的基本规则¶

圆角矩形 表示算法的"开始"与"结束
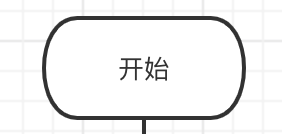
矩形表示普通的操作环节（比如计算，赋值等操作）
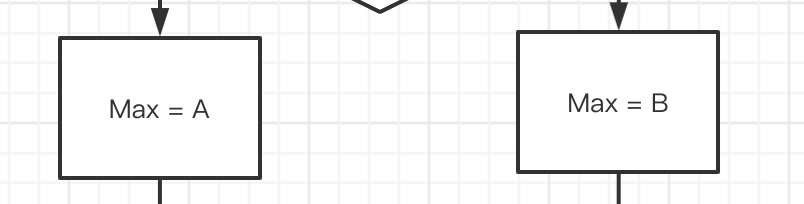
菱形表示需要进行比较、判断的环节。（比如分支结构中的判断，循环结构中的判断等）
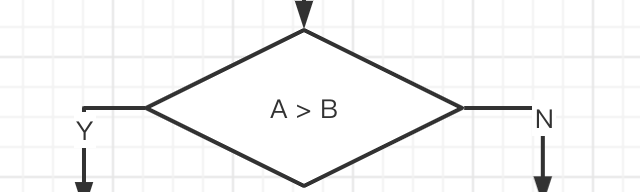
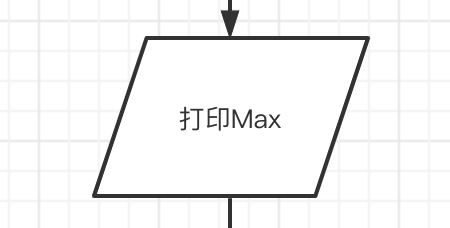
平形四边形 和数据相关，一般用于表示输入与输出。
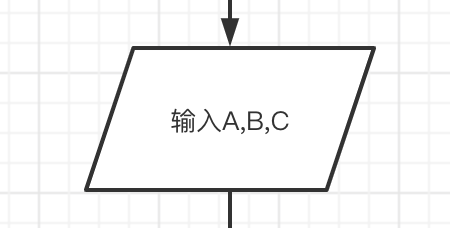
连线连线一般都带有箭头，表明流程的流动方向。在菱形出来的连线中，可以在线上标明判断后的结果，以表明不同结果的流动方向。

13.3.2.2 三种结构的流程图示例¶

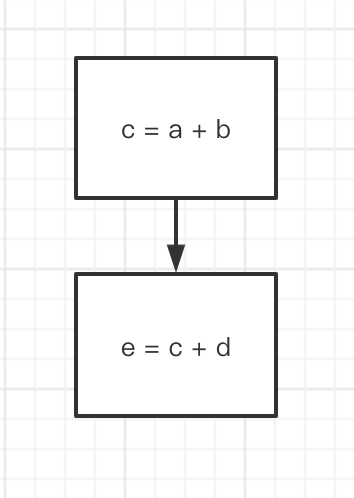
顺序结构：我们只需要将两个环节用带箭头的线连接起来即可。请看下面的例子：
```
c = a + b
e = c + d
```
对应流程图为：
分支结构: 需要使用菱形块来达到分支结构。
```
if a % 2 == 0:
    c = a + 2
else:
    c = a * 2
```
对应流程图为

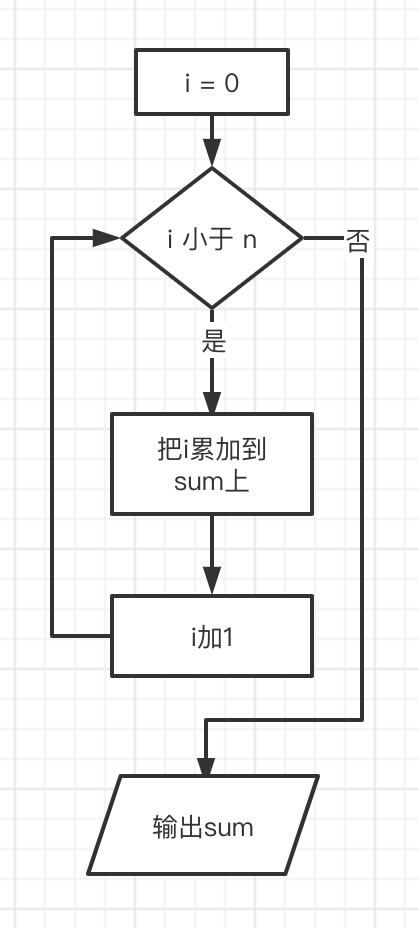
循环结构: 使用菱形块来达到循环结构

n = int(input())
sum = 0
i = 0
while i < n:
    sum += i
    i += 1
print(sum)

对应流程图为：

小练习

请根据以下的算法流程图，写出对应的Python语句

13.4 如何评价一个算法的好坏？¶

正确与否: 首先我们要确定算法能产生正确的结果。
容错性好（健壮性好）：就是在处理一些非法输入时，算法不会造成程序崩溃，而能给予良好的提示。
算法的效率高且占用空间少
时间复杂度 运算占用的时间低。通常我们会使用算法中比较耗费CPU时间的操作的出现次数来衡量算法时间复杂度的高低。一般一个算法会讨论以下两个问题：最坏情况下和平均的时间复杂度。下面会用简单的例子来演示如何进行算法时间分析。
空间复杂度 算法的空间复杂度是指算法需要消耗的空间资源。这个分析会比时间复杂度的分析容易许多。
是否易读

13.4.1 时间复杂度分析示例¶

以查找算法为例，我们简单分析两种算法的时间复杂度（顺序查找、符号表查找）。

算法1. 顺序查找

def find(array, target):
    i = 0
    while i < len(array):
        if array[i] == target:
            print("{} is located at index {}".format(target, i))
            break
        i += 1

最坏情况下的时间查找次数

我们使用 \(N\) 表示数组的长度。很简单可以得出最坏情况下的比较次数(即没有查找到目标数)为 \(N\) 次
平均查找次数

我们假设待查找数字在每个位置出现的概率是相同的，简单的，我们可以得出当target在位置i处，那么算法需要i次比较后才能找到该数。所以这样就可以把target在每个位置i可能出现情况下，所需要比较的次数加和后，再除以总的可能情况数 \(N+1\)（同时还有没有找到目标数这种情况）就能得到平均查找次数了。

\[\bar{T} = \frac{1}{N+1} \sum_{i=0}^{N}i = \frac{N}{2}\]

思考题请你分析以下的算法复杂度。

算法2: 符号表查找

sym = [ [] for i in range(10000)]
sym_initialized = False

def find(array, target):
    global sym
    global sym_initialized

    if not sym_initialized:
        i = 0
        while i < len(array):
            sym[array[i]].append(i)
        sym_initialized = True

    return array[target]

请写出什么情况下是最坏情况？其比较次数是多少？
请写出平均比较次数是多少？

第13课 算法分析基础¶